Como utilizar o teste t de student
Talvez o teste de hipótese mais conhecido, o teste t de Student pode ser utilizado para avaliar se há diferença significativa entre as médias de duas amostras. Sua simplicidade e a fácil implementação em softwares o tornou tão popular, mas por outro lado também tornou comum o seu uso de maneira incorreta. Esta publicação é um pequeno guia de como usar o teste t clássico em duas amostras de maneira correta, respeitando todas suas suposições, dando alternativas quando esses pré-requisitos não são possíveis e um exemplo de como implementar no R.
O que eu preciso para poder usar o teste t?
Essa é uma pergunta que você como estudante, pesquisador ou analista sempre deve fazer ao utilizar qualquer ferramenta matemática: “Quais são as suposições para aplicar a ferramenta? Quais as hipóteses?” No caso do teste de hipótese, quais a suposições acerca dos dados eu devo conferir antes de realizá-lo?
Feita a pergunta, seguem as suposições a serem verificadas para realizar o teste t em duas amostras independentes:
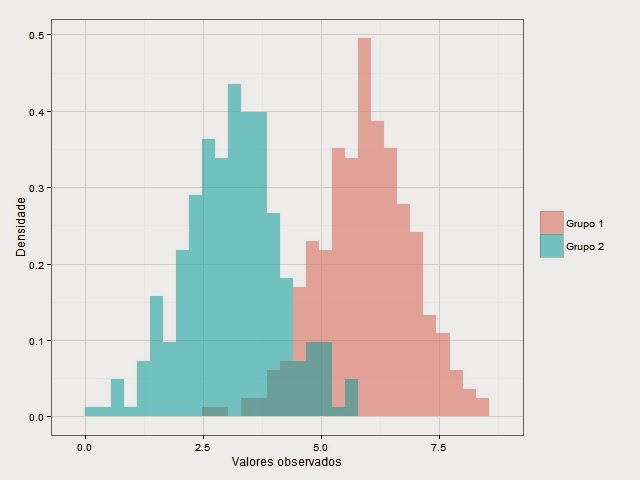
- As duas amostras devem ter distribuição normal. Pode-se verificar utilizando o teste de Shapiro Wilk ou observando os dados dispostos em um qqplot.
- As duas amostras devem ter mesma variância. Pode-se verificar observando o desvio padrão amostral das duas amostras ou utilizando um teste F de igualdade de variâncias.
- As duas amostras devem ser independentes. Depende de como o experimento foi delineado. Note que apenas calcular a correlação entre as duas amostras pode não ser suficiente. É preciso saber como os dados foram coletados.
Caso tenha apenas uma amostra, a única suposição é que tenha distribuição normal.
Unicaudal ou bicaudal? Como interpretar?
Unicaudal e bicaudal são termos diretamente ligados às hipóteses nula e alternativa. Usualmente, os pesquisadores definem a hipótese nula como sendo médias iguais para as duas amostras. Caso a hipótese alternativa seja a média de uma amostra maior que a média da outra amostra, então temos um teste unicaudal. Caso a hipótese alternativa seja apenas médias diferentes, temos um teste bicaudal.
Um dos resultados do teste é o p-valor. Se o nível do teste for 5%, como amplamente utilizado pelos pesquisadores, um p-valor abaixo de 0.05 dá evidências a favor da hipótese alternativa. Caso a hipótese nula seja a usual, médias iguais, p-valor abaixo de 0.05 dá indícios de que são diferentes, mas sempre em função da hipótese alternativa. Porém, cuidado ao tirar conclusões apenas a partir do p-valor. Uma publicação anterior mostra os cuidados que você deve tomar ao estudar o p-valor.
Caso as suposições não sejam adequadas aos seus dados ou não há segurança para suportá-la, como no caso de pequenas amostras, uma alternativa são os testes não paramétricos, como o teste de Mann-Whitney. Este teste mencionado tem apenas a suposição de que os dados sejam contínuos.
Como implementar?
Eu utilizo o software R por ser de graça e ter uma comunidade bem participativa e cooperativa. No R, considerando que tenho duas amostras denominadas amostra1 e amostra2, pode-se utilizar o seguinte código para uma análise simples
# Verificar se são normais
qqplot(amostra1); qqline(amostra1)
qqplot(amostra2); qqline(amostra2)
# Verificar se as variâncias são iguais
var(amostra1) ; var(amostra2)
var.test(amostra1, amostra2)
# Teste t
t.test(amostra1, amostra2, alternative = 'two.sided')
Em alternative você define se o teste é unicaudal ou bicaudal. Veja o manual da função para maiores informações. A saída da função é mostrada com um exemplo abaixo. Nela você pode utilizar o p-valor e o intervalo de confiança para tirar suas conclusões.
Welch Two Sample t-test
data: amostra1 and amostra2
t = 34.6364, df = 597.222, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
2.664957 2.985338
sample estimates:
mean of x mean of y
5.944105 3.118957
E como eu faço no Excel?
No Excel ou em qualquer outro software de planilhas pode ser mais fácil do que imagina. Aqui na SOS Estatística você tem acesso gratuito a uma planilha gratuita para calcular o teste t.
Veja no vídeo abaixo como é fácil utilizar e logo em seguida clique no link para baixar.
Clique aqui ou no botão abaixo para obter sua planilha gratuitamente. Você será levado para uma outra página, mas não se preocupe que é tudo em um ambiente seguro.
Se tiver alguma dúvida, é só responder ao email que você receberá com a planilha!
Bons estudos!


22 comentários
e o teste t para comparações múltiplas, qual a tua opinião a respeito?
tenho tido alguns problemas com revisores que aprenderam que esse teste só é feito para 2 grupos, como no post, e dizem que está errado para mais de 2 médias
como uso o SAS, o comando DIFF do lsmeans, por default, faz o teste t
Obrigada!
O teste t não é adequado para comparações múltiplas, em virtude do aumento da probabilidade de ocorrência do erro tipo I. Nesses casos, o ideal é utilizar a análise de variância (ANOVA).
Olá! Eu nunca vi a utilização do teste t para comparação de mais de duas amostras ou grupos. Quando temos esse caso analisamos a soma de quadrados como se faz na ANOVA, por exemplo. Por favor, informe qual procedure e como você está utilizando o comando do SAS.
Dando uma olhada rápida aqui, pelo o que eu entendi a opção DIFF do LSMEANS faz comparações dois a dois (pairwise).
Oi! isso, comparações múltiplas, dois a dois, como Tukey, por exemplo..
fazemos a anova para saber se há diferença entre os grupos e depois o teste para verificar essas diferenças
como eu mencionei, o DIFF do LSMEANS, gera o LSD, que tbm chamamos de teste t
consegui esclarecer melhor?
queria saber a tua opinião sobre isso
Acho que entendi!
Eu não recomendo utilizar apenas o teste t dois a dois para encontrar a diferença após realizar a ANOVA, pois você pode ser enganado pelo nível inflacionado do teste. Pra isso é melhor utilizar as comparações de Tukey dois a dois.
É mais seguro utilizar o teste t apenas quando se trata de apenas duas populações.
Abraços.
ok, muito obrigada, Gabriel!
No seguinte caso – Se tenho dados referente a uma correlaçao entre o tempo (em horas) de incubaçao e o numero de bacterias geradas. O t de studante pode ser usado?. Fiz uma analise de variancia e de terminei r e r2. Mas, acredito que nao cabe o t de student. Certo?
No seguinte caso – Se tenho dados referente a uma correlaçao entre o tempo (em horas) de incubaçao e o numero de bacterias geradas. O t de studante pode ser usado?. Fiz uma analise de variancia e de terminei r e r2. Mas, acredito que nao cabe o t de student. Certo?
Olá!
O seu caso é outro: você avaliando a correlação entre duas variáveis. O teste t serve para comparar uma mesma variável entre dois grupos.
No seu caso, talvez seja interessante testar se essa correlação é significativa utilizando o teste de correlação de Spearman, mas só para ter uma ideia se realmente existe essa correlação. Para tentar estudar como uma variável influencia na outra, daí seria um pouco mais complicadinho pois está lidando com dados discretos (número de bactérias).
Se tiver mais dúvidas é só responder 🙂
Abraços,
Gabriel.
Oi Gabriel,
Obrigado pela informação. Muito útil. Indo um pouco mais adiante – você sugeriu que para testar se a correlação é significativa seria interessante usar o teste de correlação de Spearman. Eu poderia, alternativamente, usar tabelas prontas para esta comparação – tipo numero de pares e o valor do coeficiente de correlação r de Pearson com P, como coloco abaixo?
Titulo da tabela – “Valor absoluto mínimo para o coeficiente de correlação r de Pearson ser significativo”.
Texto que eu redigi: – “Na figura 13, onde os dados de todos os fermentos foram analisados simultaneamente, o valor de R2 foi 0,746, correspondendo ao valor r de 0,863. Nesse caso especificamente, considerando-se o número de pares correlacionados (n=22) (BARBETTA; REIS; BORNI, 2004, pg. 407; Anexo A) ou o grau de liberdade da amostra (Glib=20) (DORIA FILHO, 1999, pg. 125; ANEXO B), observa-se que o r obtido ocorreu para p < 0,01 e, consequentemente, pode-se considerar que há uma correlação estatisticamente significativa (BARBETTA; REIS; BORNI, 2004 – pp. 316-351)”.
Mais uma vez obrigado,
Artur
Oi, Artur!
Eu acho que é muito mais simples do que isso. Sinceramente, não entendi muito bem o que está escrito. Seu r é o coeficiente de correlação? E o R^2 é o valor resultante de uma regressão? Se for, quais são as variáveis da regressão?
Abraços,
Gabriel.
Gabriel, poderia me ajudar? Preciso aplicar um teste em um trabalho de estatística aplicada a psicologia. O projeto refere-se a aplicação de biblioterapia em crianças hospitalizadas, ou seja, uso da leitura. Nisso, dividiria as crianças em dois grupos. Grupo A – aplicação de biblioterapia e Grupo B – não aplicação. E depois, 4 questionários em ambos os grupos para analisar as mudanças comportamentais nos quesitos: I – humor; II – impacto do tratamento; III – estado de tensão e IV – aceitação da doença. Como eu aplicaria um teste nesse caso? Seria a ANOVA seguida do T- student? Att, Jéssica Aguiar.
Oi, Jéssica.
Eu preciso entender melhor como são essas perguntas dos questionários e saber qual o seu objetivo. Você quer avaliar se há diferença nas respostas entre os grupos? Lembre-se que eu só posso aplicar o teste t se minha variável for contínua. Se for uma variável categórica, como respostas de questionário que vão de 1 a 5, preciso utilizar outra ferramenta, talvez um teste chi quadrado.
Abraços.
Olá, eu preciso analisar uma variavek numérica,que é uma "nota" de um questionario sobr rinite alergica de 20 pacientes, pré e pós-operatório, ou seja, em duas ocasioes diferentes.
Seria uma amaostra pareada, certo?
eu preciso ter o valor de t e o valor de p, certo?
como eu posso realizar isso usando o excel? vc sabe?
e usando o software stata?
obrigada
que testes são subdivididos do teste T
Como assim?
Olá,
Tenho dificuldade em entender a hipótese nula e alternativa.
Agradeço se puder me ajudar.
Oi, Rebeca.
É muito mais simples do que imagina: a hipótese nula é o que você assume verdade e a hipótese alternativa é o que você vai testar contra essa “verdade”. Por exemplo, em um julgamento o réu é inocente até que se prove o contrário. Então, a hipótese nula é a inocência do indivíduo e a alternativa é que ele é culpado. As argumentações da acusação e defesa que darão evidências a favor de uma das hipóteses.
Talvez esta publicação lhe ajude a entender melhor: https://manipulandodados.com.br/entendendo-erro-tipo-i-e-erro-tipo-2/
Olá,
Qual a diferença do teste t e do teste t pareado?
Agradeço desde já.
Oi, Rebeca.
O teste t comum é usado quando queremos testar a média de dois grupos independentes. Por exemplo, altura de homens e mulheres, já que homens e mulheres são dois grupos independentes. O teste t pareado é usado quando quero testar uma variável de um mesmo indivíduo. Por exemplo, testar o nível médio de colesterol de indivíduos antes de um tratamento e depois do tratamento. Neste caso, as variáveis colesterol_antes e colesterol_depois são de uma mesma pessoa e essa informação deve ser levada em consideração, já que não são independentes.
Com que objetivo se utiliza o teste t de Student em pesquisas e testes psicológicos?
Oi, Luiza.
Depende do estudo. O teste t é para variáveis quantitativas, então qualquer pesquisa que envolva esse tipo de variável o teste pode ser usado para comparar a média de dois grupos.