Como fazer teste Chi Quadrado de Pearson no Excel

Para você que viu como usar o teste Chi Quadrado de Pearson na semana passada e ficou se perguntando como é que eu faço o teste Chi Quadrado no Excel, este post é para você.

Como sempre reforço, o Excel não é a principal ferramenta computacional usada pelos estatísticos. Nós preferimos o R, Python e outras linguagens de programação com maior potencial de desenvolvimento do que o Excel. Porém, para o usuário que não estuda, mas apenas utiliza as ferramentas estatística, o Excel pode ser bem útil. Portanto, vamos lá!

NOTA: Se você quer aprender sobre o teste e como interpretar, recomendamos antes a leitura do post Teste Chi Quadrado de Pearson e tabelas de contingência, e daí depois partir para a aplicação no Excel.

Planilhas auxiliares

Para realizar o seu teste Chi Quadrado de Pearson no Excel vamos disponibilizar duas planilhas que irão lhe auxiliar a calcular se há relação entre duas variáveis categóricas ou não. Como há várias versões de Excel, disponibilizamos um arquivo em .XLS e outro em .XLSX para que você possa usar até mesmo naquele Excel velho que tem mais de 10 anos, rs.

• Planilha para teste Chi Quadrado de Pearson em Excel (<2007) .XLS
• Planilha para teste Chi Quadrado de Pearson em Excel (atual) .XLSX

Abaixo segue um exemplo do que você irá baixar. Eu utilizo o Excel 2016 para MAC OSX, então se você usar o Windows pode ser que tenha uma diferença de visual, mas as funções são as mesmas.

Planilha auxiliar preenchida com os dados do exemplo de canhotos e destros distribuídos por sexo.

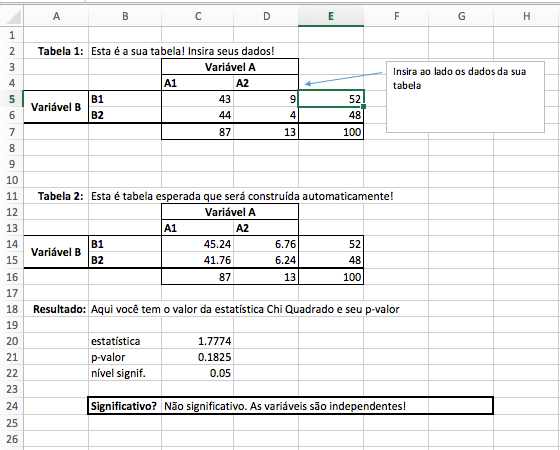
Baixadas as planilhas acima, vamos ver como usá-las e como realizar o teste de hipótese.

Teste Chi Quadrado de Pearson no Excel

Como você pode ver na figura acima e nas planilhas baixadas, temos duas tabelas e um espaço para os nossos resultados. A única coisa que você precisa fazer é inserir os seus dados na primeira tabela (que vem em branco no download). Só isso! O resto a planilha faz para você.

Resumindo, temos:

• Tabela 1: espaço para você inserir os seus dados.
• Tabela 2: gerada automaticamente, não precisa se preocupar com ela. Serve para fazer o cálculo do p-valor.
• Resultados: Espaço para a estatística Chi Quadrado resultante, p-valor e nível de significância (deixado em 0,05) para verificar se podemos rejeitar a hipótese de independência ou não. O nível de significância pode ser ajustado conforme sua necessidade.

E para tabelas acima de 2×2?

Note que esta planilha serve apenas para tabelas 2×2, porém o teste serve para qualquer tabela n por m, para n,m inteiros. Por exemplo, uma tabela 4×2, 5×3, etc.

Neste caso, só adicionar uma coluna na planilha auxiliar não irá funcionar. Se você tem uma familiaridade com o Excel verá que pode replicar o que foi feito na tabela 2×2 para uma tabela MxN no sentido que terá que gerar uma tabela de valores esperados e depois utilizar a função CHITEST. Para auxiliar, temos os seguintes passos que você pode seguir.

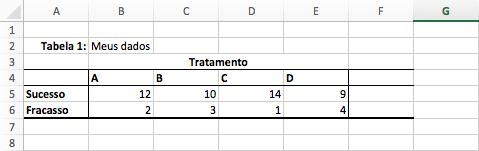
1. Insira sua tabela no Excel

Insira sua tabela maior que 2×2 no Excel, como na figura abaixo. Neste exemplo, estamos utilizando uma 2×4, com 4 colunas e 2 linhas.

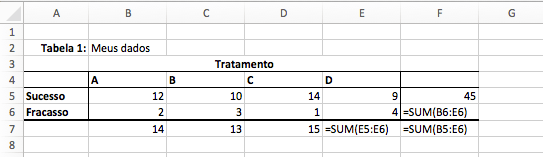
2. Calcule as frequências marginais

Basta somar todas as frequências de linhas, colunas e total, como na figura abaixo. Nas células estão um exemplo da função SUM (ou soma, em português).

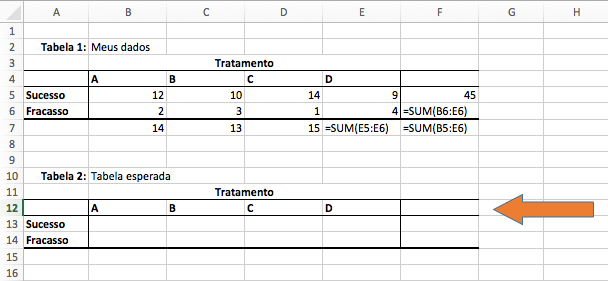
3. Crie o espaço para a tabela esperada

Esta tabela esperada será utilizada para calcular o p-valor do teste. No nosso exemplo, como a tabela inserida foi de tamanho 2×4, reservamos um espaço também de tamanho 2×4.

4. Calcule o valor esperado para cada célula

O valor esperado E é dado pela multiplicação das marginais de linhas e colunas dividido pelo total. Ou seja,

E = (Total linha) x (Total coluna) / Total

Isso deve ser feito para cada célula com seu respectivo total marginal, como na figura abaixo realçando o que deve ser multiplicado e o que deve ser dividido.

5. Calcule o p-valor (aleluia!)

Depois de construídas as tabelas é só usar a função CHITEST que ela calcula o p-valor automaticamente.

Neste exemplo, o p-valor encontrado foi de 0,3803 indicando que a hipótese de independência não pode ser rejeitada.

Se este post lhe foi útil, recomende para algum coleguinha ou deixe seu like. Se ainda assim tiver dúvidas, pergunte aqui nos comentários.